Un peu de géométrie projective
Projection conique, perspective et géométrie projective : comment passer d’un plan à un autre.
(article écrit en 2007)
Quel est le problème
Étant donnée la photographie d’une partie de billard, comment faire pour retrouver les positions réelles des boules ?
La question initiale (formulée autrement) a été posée par Jean-Luc Frantz sur le forum nzn.fr.delphi. S’en est suivi un échange entre lui, Emmanuel Bresson et moi-même, et je présente ici l’une des solutions.
Le champ d’application de cette solution dépasse le cadre de la question de départ, puisqu’il s’agit de pouvoir passer d’un plan à un autre dans le cadre de la géométrie projective.
Or la géométrie projective correspond à la vision que nous avons du monde (du moins mieux que la perspective cavalière) ; elle correspond aussi à ce qu’on appelle perspective conique, souvent utilisée en art. Elle est exactement la traduction de ce que donne une photographie.
Par exemple, le problème consistant à raccorder entre elles 2 photographies aériennes d’un même lieu, prises depuis des endroits différents et inconnus, trouve une solution dans ce qui suit.
La situation

On connaît la position précise (au ½ mm près) de 10 points du billard.
Ces repères sont appelés “mouches”, et on les désigne ici par gbgN (pour grande bande gauche), gbdN (pour grande bande droite) et pbbN (pour petite bande bas).
Le billard possède un repère “naturel”, avec pour origine le coin inférieur gauche. L’unité est le mm.
Pour la photo, on repère la position d’un point en pixels (origine en haut à gauche).
La photo ci-dessus a été réduite 3 fois, mais voici le tableau des coordonnées dans les 2 cas :
| Point |
Billard (en mm) |
Photo (en pixels) |
| pbb1 | (439, 0) | (250, 559) |
| pbb2 | (1150, 0) | (662, 564) |
| gbg1 | (0, 439) | (58, 426) |
| gbg2 | (0, 794) | (95, 344) |
| gbg3 | (0, 1150) | (126, 275) |
| gbg4 | (0, 1506) | (154, 218) |
| gbd1 | (1589, 439) | (852, 436) |
| gbd2 | (1589, 794) | (814, 352) |
| gbd3 | (1589, 1150) | (784, 284) |
| gbd4 | (1589, 1506) | (757, 227) |
| Boule entourée | (?, ?) | (337, 215) |
Les coordonnées sur la photo souffrent malheureusement d’une imprécision de l’ordre de 5 pixel.
L’exemple à télécharger (à la fin de la page) calcule les coordonnées réelles de la boule entourée.
Mais avant, il faut se plonger un peu dans les maths pour y comprendre quelque chose…
Solution : explications théoriques.
La solution présentée nécessite la résolution de 5 systèmes de 3 équations à 3 inconnues.
Je m’appuie sur “Géométrie” de Marcel Berger (un classique pour les matheux).
Les extraits du livre sont en citations et je les commente ensuite dans l’optique du problème posé.
Les coordonnées homogènes
À tout point M (x, y) d’un plan, on associe ses coordonnées homogènes (X, Y, Z) définies par x = X / Z et y = Y / Z.
Ces coordonnées sont très utilisées en géométrie projective. Il faut bien voir que les coordonnées homogènes ne sont pas uniques, mais définies à un coefficient près. Si Z = 0, on obtient un point à l’infini.
- Pour passer des coordonnées planes aux coordonnées homogènes : (x, y) donne (x, y, 1)
- pour passer des coordonnées homogènes aux planes : (X, Y, Z) donne (X / Z, Y / Z).
Définition d’un espace projectif
Soit E un espace vectoriel sur un corps K.
On appelle espace projectif déduit de E, et l’on note P(E) le quotient (E \ 0) / R par la relation d’équivalence R : xRy ssi y = kx pour k dans K.
La dimension de P(E) est par définition dim E - 1.
La projection canonique est p : E \ 0 —> P(E).
Pour nous K = IR et E est un espace réel de dimension 3. P(E) est de dimension 2 (plan projectif).
Si (x0, x1, x2) sont les coordonnées de x dans une base (ei) de E, alors (x0, x1, x2) seront les coordonnées homogènes de m = p(x) par rapport à cette base (de E ; pas encore de nos bases “locales”).
Définition d’un repère projectif
Soit P(E) un espace projectif de dimension n.
On appelle repère projectif de P(E) un système {mi} (i = 0, …, n+1) de n+2 points de P(E) tel qu’il existe une base {ei} (i = 1, …, n+1) de E tel que mi = p(ei) (pour i = 1, …, n+1) et m0 = p(e1 + … + en+1).
{m0, m1, m2, m3} sera donc un repère projectif d’un plan projectif si on trouve une base {e1, e2, e3} de l’espace ℝ3 tel que p(e1) = m1, p(e2) = m2, p(e3) = m3 et p(e1 + e2 + e3) = m0.
Voilà pourquoi il faudra 4 points.
Cette définition semble imposer au point m0 d’être spécial, mais heureusement Berger montre par ailleurs que les repères correspondent à des sommets de quadrilatères (4 points dont 3 ne sont jamais alignés), et il montre même comment fabriquer la base {ei} de ℝ3 à partir des {mi} dans la démonstration d’une autre propriété :
Choisissons des ei dans E tels que p(ei) = mi (i = 0, 1, …, n+1).
Puisque les {mi} (i = 1, …, n+1) sont indépendants, {ei} (i = 1, …, n+1) est une base de E.
Écrivons e0 = k1 e1 + … + kn+1 en+1.
Le fait que les {mj} (pour j <> i et i = 1, …, n+1) soient indépendants se traduit par ki <> 0.
Donc {ki ei} (i = 1, …, n+1) est encore une base de E, et satisfait la définition.
Remarquons au passage que les ki sont donc tous non nuls.
Il définit ensuite les morphismes et isomorphismes d’espaces projectifs, les isomorphismes étant appelés homographies, comme correspondants aux morphismes et isomorphismes de E par passage au quotient.
Il est clair qu’on a affaire à une homographie.
On arrive au :
Premier théorème fondamental de la géométrie projective
Soient P(E) et P(E’), 2 espaces projectifs de même dimension finie et {mi}, {m’i}, 2 repères projectifs de P(E) et P(E’) respectivement.
Alors il existe une homographie unique g : P(E) —> P(E’) tel que g(mi) = m’i pour tout i.
Ce théorème assure que le problème a une solution.
Pour la trouver, partant des 4 points de chaque plan (les {mi} et {m’i}), il faudra fabriquer les repères {ei} et {e’i} de ℝ3 qui vont avec, puis trouver la matrice 3x3 traduisant l’isomorphisme de ℝ3 associé à la solution cherchée.
Solution : explications pratiques.
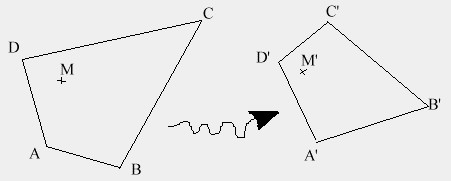
On cherche l’homographie qui transforme le quadrilatère ABCD en le quadrilatère A’B’C’D’, connaissant les coordonnées de ces 8 points dans les repères choisis pour chacun des 2 plans.
Pour tout point M du premier plan, on veut pouvoir calculer les coordonnées de son image M’ dans l’autre plan.
Je note $\begin{pmatrix}x_{A} \\y_{A} \end{pmatrix}$ les coordonnées “locales” du point A.
Les vecteurs $\begin{pmatrix}x_{A} & y_{A} & 1\end{pmatrix}$, $\begin{pmatrix}x_{B} & y_{B} & 1\end{pmatrix}$ et $\begin{pmatrix}x_{C} & y_{C} & 1\end{pmatrix}$ forment une base de ℝ3.
Pour trouver la base {ei}, on résout le premier système : $\begin{pmatrix}x_{A} & x_{B} & x_{C} \\ y_{A} & y_{B} & y_{C} \\ 1 & 1 & 1 \end{pmatrix}\begin{pmatrix}k_{1} \\ k_{2} \\ k_{3}\end{pmatrix}=\begin{pmatrix}x_{D} \\ y_{D} \\ 1\end{pmatrix}$ dont les inconnues sont les 3 coefficients k1, k2 et k3.
De même, on doit résoudre le second système : $\begin{pmatrix}x'_{A} & x'_{B} & x'_{C} \\ y'_{A} & y'_{B} & y'_{C} \\ 1 & 1 & 1 \end{pmatrix}\begin{pmatrix}k'_{1} \\ k'_{2} \\ k'_{3}\end{pmatrix}=\begin{pmatrix}x'_{D} \\ y'_{D} \\ 1\end{pmatrix}$ correspondant au second plan.
On aura en fait seulement besoin des 3 rapports $R_{1}=\frac{k'_{1}}{k_{1}}$, $R_{2}=\frac{k'_{2}}{k_{2}}$ et $R_{3}=\frac{k'_{3}}{k_{3}}$ (les ki sont non nuls).
J’appelle Mat la matrice 3x3 traduisant l’isomorphisme de ℝ3 associé à l’homographie cherchée.
$$\mathit{Mat}=
\begin{pmatrix}
a_{1}^{1} & a_{2}^{1} & a_{3}^{1} \\
a_{1}^{2} & a_{2}^{2} & a_{3}^{2} \\
a_{1}^{3} & a_{2}^{3} & a_{3}^{3}
\end{pmatrix}$$
Les 3 égalités matricielles e’i = Mat . ei donnent un système de 9 équations à 9 inconnues (les coefficients de la matrice).
Mais ce système peut être séparé en 3 systèmes de 3 équations à 3 inconnues :
$$\begin{pmatrix}x_{A}&y_{A}&1 \\ x_{B}&y_{B}&1 \\ x_{C}&y_{C}&1\end{pmatrix}
\begin{pmatrix}a_{1}^{1} \\ a_{2}^{1} \\ a_{3}^{1}\end{pmatrix}=
\begin{pmatrix}R_{1}x'_{A}\\ R_{2}x'_{B} \\ R_{3}x'_{C}\end{pmatrix}$$
$$\begin{pmatrix}x_{A}&y_{A}&1 \\ x_{B}&y_{B}&1 \\ x_{C}&y_{C}&1\end{pmatrix}
\begin{pmatrix}a_{1}^{2} \\ a_{2}^{2} \\ a_{3}^{2}\end{pmatrix}=
\begin{pmatrix}R_{1}y'_{A} \\ R_{2}y'_{B} \\ R_{3}y'_{C}\end{pmatrix}$$
$$\begin{pmatrix}x_{A}&y_{A}&1 \\ x_{B}&y_{B}&1 \\ x_{C}&y_{C}&1\end{pmatrix}
\begin{pmatrix}a_{1}^{3} \\ a_{2}^{3} \\ a_{3}^{3}\end{pmatrix}=
\begin{pmatrix}R_{1} \\ R_{2} \\ R_{3}\end{pmatrix}$$
Étant donné alors un point M $\begin{pmatrix}x_{M} \\ y_{M}\end{pmatrix}$ du premier plan, on calculera d’abord les coordonnées homogènes $\begin{pmatrix}X \\ Y \\ Z\end{pmatrix}$ de son image M’ par la formule
$$\begin{pmatrix}X \\ Y \\ Z\end{pmatrix}=\mathit{Mat}.\begin{pmatrix}x_{M} \\ y_{M} \\ 1\end{pmatrix}.$$
On aura enfin : $x'_{M}=\frac{X}{Z}$ et $y'_{M}=\frac{Y}{Z}$.
Exemple
projectif.zip (executable + sources Delphi)
Dernière modification de cette page : 2018-11-09.