Context help
The tiling
The tiling is a regular filling of the plane, done with a single figure.

The basic figure is the tile:

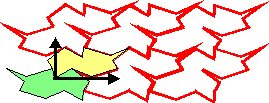
The fundamental set of tiles is a group of several tiles which allows to do the tiling in 2 directions of translations:

Fundamental set of tiles
The fundamental set of tiles is a group of several tiles which allows to do the tiling in 2 directions of translations.

Tile
The tile is the basic element for a tiling

As a tile is in contact with another, each part of its contour appears twice.

Group of displacement
Each type of tiling is associated to a group of displacement of the plane. This group is made of the displacement allowing to go from one tile to another.
The displacements are:
- The translations
- The rotations
- The central symmetries
- The axial symmetries
- The glide reflections
The groups associated to a different type of tiling are always the results of a finite number of displacements, within which are 2 translations.
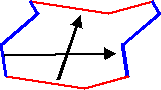
Translations

In a translation, you displace the figure without turning it over or upside down.
The translation is represented by an arrow called vector.
The 2 translations associated to each tiling allow to go from one fundamental set of tiles to another.

Rotations
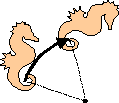
In a rotation, the figure turns around a point called center.
It is also necessary to know the angle of rotation.
The rotations associated to a tiling always have their angles being equal to:
- 1/6 of rotation and multiple angles (2/6=1/3, 3/6=1/2, 4/6=2/3 and 5/6)

- 1/4 of rotation and multiple angles (2/4=1/2 and 3/4)

- 1/3 of rotation and multiple angles (2/3)

- 1/2 of rotation (these are central symmetries)

The centers of rotation are always on the contour of the tile:

Central symmetries

A central symmetry is a rotation the angle of which is a 1/2 turn.
Axial symmetries

In an axial symmetry, the figure is turned around an axis.
When a tiling has an axis of symmetry, a part of the contour of the tile is along this axis and cannot be distorted.

The tilings with several directions of angles of symmetry, often have a fixed contour:

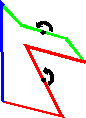
Glide reflections

You can get a glide reflection if you compose an axial symmetry with a translation the vector of which is parallel to the axis of symmetry.
Group
A group is a set (let us call it G) with a law of internal composition (if x and y are parts of G , x¤y too) associative (x ¤ y) ¤ z = x ¤ (y ¤ z),We can then write x¤y¤z) as a neutral element exists (e is the neutral element if, for each x, we’ve got x ¤ e = e ¤ x = x) and if each element has an inverse (reciprocal) (for each x , y exists as x ¤ y = y ¤ x = e).
Examples: * the integers (positive or negative) form a group for addition (the neutral element is zero and the opposite (additive inverse) of 5 is -5 * however, positive integers , don’t form a group for addition * the displacements of the plane form a group for composition.
Composition
The composition of two displacements of the plane consists in doing two displacements one after the other.
Example:
- The composition of two translations is a translation:

- The composition of a translation and a rotation is a rotation:

- The composition of two axial symmetries is a translation or a rotation:


The 17 types of tilings
Type nb 1: p1
(asymmetric parallelogramic)

The fundamental set of tiles is made of a single tile:

The group of displacement is generated by only two translations.
The contour of the tile has got 2 parts:
Type nb 2: p2
(symmetric parallelogramic)

The fundamental set of tiles is made of 2 tiles:

The group of displacement is generated by

The contour of the tile has got 4 parts:

Type nb 3: p3
(hexagonal 3-rotative)

The fundamental set of tiles is made of 3 tiles and both the vectors form an equilateral triangle:

The group of displacement is generated by
- 2 translations
- a rotation (1/3 of a turn)

The contour of the tile has got 3 parts:

Type nb 4: p4
(square 4-rotative)

The fundamental set of tiles is made of 4 tiles, and both the vectors form a half square:

The group of displacement is generated by
- 2 translations
- a rotation (1/4 of a turn)

The contour of the tile has got 3 parts:

Type nb 5: p6
(hexagonal 6-rotative)

The fundamental set of tiles is made of 6 tiles, and both the vectors form an equilateral triangle:

The group of displacement is generated by
- 2 translations
- a rotation (1/6 of a turn)

The contour of the tile has got 3 parts:

Type nb 6: pg
(gliding rectangular)

The fundamental set of tiles is made of 2 tiles, and both the vectors form a half rectangle:
The group of displacement is generated by

The contour of the tile has got 3 parts:

Type nb 7: pgg
(bi-gliding rectangular)

The fundamental set of tiles is made of 4 tiles, and both the vectors form a half rectangle:

The group of displacement is generated by

The contour of the tile has got 4 parts:

Type nb 8: pm
(mono-symmetric rectangular)

The fundamental set of tiles is made of 2 tiles, and both the vectors form a half rectangle:

The group of displacement is generated by

The contour of the tile has got 2 parts:

Type nb 9: cm
(mono-symmetric rhombic)

The fundamental set of tiles is made of 2 tiles, and both the vectors form an isosceles triangle:

The group of displacement is generated by

The contour of the tile has got 3 parts:

Type nb 10: pmg
(symmetric gliding
rectangular)
The fundamental set of tiles is made of 4 tiles, and both the vectors form a half rectangle:

The group of displacement is generated by

The contour of the tile has got 3 parts:
Type nb 11: pmm
(bi-symmetric rectangular)

The fundamental set of tiles is made of 4 tiles, and both the vectors form a half rectangle:
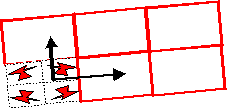
The group of displacement is generated by

The contour of the tile is a rectangle.
Type nb 12: cmm
(bi-symmetric rhombic)

The fundamental set of tiles is made of 4 tiles, and both the vectors form an isosceles triangle:

The group of displacement is generated by

The contour of the tile has got 3 parts:

Type nb 13: p4g
(gliding 4-rotative square)

The fundamental set of tiles is made of 8 tiles, and both the vectors form a half square:

The group of displacement is generated by
- 2 translations
- an axial symmetry
- a rotation (1/4 of a turn)

The contour of the tile has got 2 parts:

Type nb 14: p3m1
(tri-symmetric hexagonal)

The fundamental set of tiles is made of 6 tiles, and both the vectors form an equilateral triangle:

The group of displacement is generated by
- 2 translations
- an axial symmetry
- a rotation (1/3 of a turn)

The contour of the tile is an equilateral triangle.
Type nb 15: p31m
(symmetric 3-rotative hexagonal)

The fundamental set of tiles is made of 6 tiles, and both the vectors form an equilateral triangle:
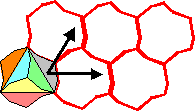
The group of displacement is generated by
- 2 translations
- an axial symmetry
- a rotation (1/3 of a turn)

The contour of the tile has got 2 parts:

Type nb 16: p4m
(totally symmetric square)

The fundamental set of tiles is made of 8 tiles, and both the vectors form a half square:

The group of displacement is generated by
- 2 translations
- an axial symmetry
- a rotation (1/4 of a turn)

The contour of the tile is a right and isosceles triangle (half square).
Type nb 17: p6m
(totally symmetric hexagonal)

The fundamental set of tiles is made of 12 tiles, and both the vectors form an equilateral triangle:

The group of displacement is generated by
- 2 translations
- an axial symmetry
- a rotation (1/6 of a turn)

The contour of the tile is a right triangle, the angles are 30°, 60° and 90°.
Last modification of this page: 2021-02-18.