Aide contextuelle
Pavage
Un pavage est un remplissage régulier du plan, réalisé avec une figure unique.

La figure de base s’appelle le pavé :

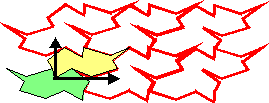
L’ensemble fondamental de pavés est un groupe de plusieurs pavés qui permet de réaliser le pavage avec deux directions de translations :

Ensemble Fondamental de Pavés
L’ensemble fondamental de pavés est un groupe de plusieurs pavés qui permet de réaliser le pavage avec deux directions de translations :

Pavé
Le pavé est l’élément de base d’un pavage.

Comme un pavé est en contact avec d’autres pavés, chaque partie de son contour se retrouve 2 fois :

Groupe de Déplacements
Chaque type de pavage est associé à un groupe de déplacements du plan. Ce groupe est constitué par les déplacements permettant de passer d’un pavé à un autre.
Les déplacements sont :
- les translations
- les rotations
- les symétries centrales
- les symétries axiales
- les glissages
Les groupes associés aux différents types de pavages sont toujours engendrés par un nombre fini de déplacements, dont 2 translations.
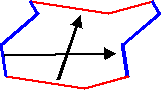
Translations

Dans une translation, on déplace la figure sans la tourner ni la retourner.
La translation est représentée par une flèche appelée vecteur.
Les 2 translations associées à tout pavage permettent de passer d’un ensemble fondamental de pavés à un autre :

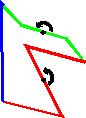
Rotations
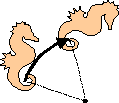
Dans une rotation, la figure tourne autour d’un point appelé centre.
On doit aussi indiquer l’angle de la rotation.
Les rotations associées à un pavage ont toujours leurs angles égaux à :
- 1/6 de tour et les angles multiples (2/6=1/3, 3/6=1/2, 4/6=2/3 et 5/6)

- 1/4 de tour et les angles multiples (2/4=1/2 et 3/4)

- 1/3 de tour et les angles multiples (2/3)

- 1/2 tour (ce sont des symétries centrales)

Les centres des rotations sont toujours sur le contour du pavé :

Symétries Centrales

Une symétrie centrale est une rotation dont l’angle est 1/2 tour.
Symétries Axiales

Dans une symétrie axiale, la figure est retournée autour d’un axe.
Lorsqu’un pavage possède un axe de symétrie, une partie du contour du pavé est située le long de cet axe, et ne peut donc être déformée :

Les pavages possédant plusieurs directions d’axes de symétrie ont souvent un contour fixe :

Glissages

Un glissage est obtenu en composant une symétrie axiale avec une translation dont le vecteur est parallèle à l’axe de la symétrie.
Groupe
Un groupe est un ensemble (notons-le G) muni d’une loi de composition interne (si x et y sont éléments de G, x ¤ y aussi) associative ((x ¤ y) ¤ z = x ¤ (y ¤ z), et on peut donc écrire x ¤ y ¤ z) telle qu’il existe un élément neutre (e est l’élément neutre si, pour tout x, on a x ¤ e = e ¤ x = x) et que tout élément ait un inverse (pour tout x, il existe y tel que x ¤ y = y ¤ x = e).
Exemples :
- les nombres entiers relatifs (positifs et négatifs) forment un groupe pour l’addition (l’élément neutre est 0, et l’inverse de 5 est -5)
- par contre, les nombres entiers positifs seuls ne forment pas un groupe pour l’addition
- les déplacements du plan forment un groupe pour la composition.
Composition
La composition de 2 déplacements du plan consiste à effectuer les 2 déplacements l’un après l’autre.
Exemples :
- La composition de 2 translations donne une translation

- La composition d’une rotation et d’une translation donne une rotation

- La composition de 2 symétries axiales donne une translation ou une rotation


Les 17 types de pavages
Type n°1 : p1
(parallélogrammique asymétrique)

L’ensemble fondamental de pavés n’est constitué que d’un seul pavé :

Le groupe de déplacements n’est engendré que par 2 translations.
Le contour du pavé possède 2 parties :
Type n°2 : p2
(parallélogrammique symétrique)

L’ensemble fondamental de pavés est constitué de 2 pavés :

Le groupe de déplacements est engendré par

Le contour du pavé possède 4 parties :

Type n°3 : p3
(héxagonal 3-rotatif)

L’ensemble fondamental de pavés est constitué de 3 pavés, et les 2 vecteurs forment un triangle équilatéral :

Le groupe de déplacements est engendré par
- 2 translations
- une rotation (1/3 de tour)

Le contour du pavé possède 3 parties :

Type n°4 : p4
(carré 4-rotatif)

L’ensemble fondamental de pavés est constitué de 4 pavés, et les 2 vecteurs forment la moitié d’un carré :

Le groupe de déplacements est engendré par
- 2 translations
- une rotation (1/4 de tour)

Le contour du pavé possède 3 parties :

Type n°5 : p6
(héxagonal 6-rotatif)

L’ensemble fondamental de pavés est constitué de 6 pavés, et les 2 vecteurs forment un triangle équilatéral :

Le groupe de déplacements est engendré par
- 2 translations
- une rotation (1/6 de tour)

Le contour du pavé possède 3 parties :

Type n°6 : pg
(rectangulaire glissant)

L’ensemble fondamental de pavés est constitué de 2 pavés, et les 2 vecteurs forment la moitié d’un rectangle :
Le groupe de déplacements est engendré par
- 2 translations
- un glissage

Le contour du pavé possède 3 parties :

Type n°7 : pgg
(rectangulaire biglissant)

L’ensemble fondamental de pavés est constitué de 4 pavés, et les 2 vecteurs forment la moitié d’un rectangle :

Le groupe de déplacements est engendré par
- 2 translations
- une symétrie centrale
- 2 glissages

Le contour du pavé possède 4 parties :

Type n°8 : pm
(rectangulaire monosymétrique)

L’ensemble fondamental de pavés est constitué de 2 pavés, et les 2 vecteurs forment la moitié d’un rectangle :

Le groupe de déplacements est engendré par
- 2 translations
- une symétrie axiale

Le contour du pavé possède 2 parties :

Type n°9 : cm
(rhombique monosymétrique)

L’ensemble fondamental de pavés est constitué de 2 pavés, et les 2 vecteurs forment un triangle isocèle :

Le groupe de déplacements est engendré par
- 2 translations
- une symétrie axiale

Le contour du pavé possède 3 parties :

Type n°10 : pmg
(rectangulaire glissant symétrique)

L’ensemble fondamental de pavés est constitué de 4 pavés, et les 2 vecteurs forment la moitié d’un rectangle :

Le groupe de déplacements est engendré par

Le contour du pavé possède 3 parties :
Type n°11 : pmm
(rectangulaire bisymétrique)

L’ensemble fondamental de pavés est constitué de 4 pavés, et les 2 vecteurs forment la moitié d’un rectangle :
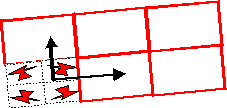
Le groupe de déplacements est engendré par

Le contour du pavé est un rectangle.
Type n°12 : cmm
(rhombique bisymétrique)

L’ensemble fondamental de pavés est constitué de 4 pavés, et les 2 vecteurs forment un triangle isocèle :

Le groupe de déplacements est engendré par

Le contour du pavé possède 3 parties :

Type n°13 : p4g
(carré 4-rotatif glissant)

L’ensemble fondamental de pavés est constitué de 8 pavés, et les 2 vecteurs forment la moitié d’un carré :

Le groupe de déplacements est engendré par
- 2 translations
- une symétrie axiale
- une rotation (1/4 de tour)

Le contour du pavé possède 2 parties :

Type n°14 : p3m1
(héxagonal trisymétrique)

L’ensemble fondamental de pavés est constitué de 6 pavés, et les 2 vecteurs forment un triangle équilatéral :

Le groupe de déplacements est engendré par
- 2 translations
- une symétrie axiale
- une rotation (1/3 de tour)

Le contour du pavé est un triangle équilatéral.
Type n°15 : p31m
(héxagonal 3-rotatif symétrique)

L’ensemble fondamental de pavés est constitué de 6 pavés, et les 2 vecteurs forment un triangle équilatéral :
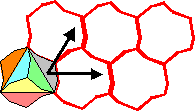
Le groupe de déplacements est engendré par
- 2 translations
- une symétrie axiale
- une rotation (1/3 de tour)

Le contour du pavé possède 2 parties :

Type n°16 : p4m
(carré totalement symétrique)

L’ensemble fondamental de pavés est constitué de 8 pavés, et les 2 vecteurs forment la moitié d’un carré :

Le groupe de déplacements est engendré par
- 2 translations
- une symétrie axiale
- une rotation (1/4 de tour)

Le contour du pavé est un triangle rectangle et isocèle (demi-carré).
Type n°17 : p6m
(héxagonal totalement symétrique)

L’ensemble fondamental de pavés est constitué de 12 pavés, et les 2 vecteurs forment un triangle équilatéral :

Le groupe de déplacements est engendré par
- 2 translations
- une symétrie axiale
- une rotation (1/6 de tour)

Le contour du pavé est un triangle rectangle d’angle 30°, 60° et 90°.
Dernière modification de cette page : 2021-02-18.